第4章  可观测量

洛仑兹变换没有可观测性，但是引入“事件”概念之后，可以从洛仑兹变换推导出时空坐标的相对量，这些相对量具有可观测性。

可观测量对于微观世界极为重要。 

4.1  电磁事件

洛仑兹变换分为两种基本变换，一种是时空坐标变换，一种是事件坐标变换，简称事件变换。

电磁事件分为时空事件和物理量事件。

事件的变换不仅引导出时空坐标的可观测性，而且引导出物理量的洛仑兹变换。

1. 电磁事件时空图

时空坐标组（x，t）代表事件。图13是时空坐标图，图中每一点代表一个事件。事件1的时空坐标和事件2的时空坐标分别标记为
               和   


        

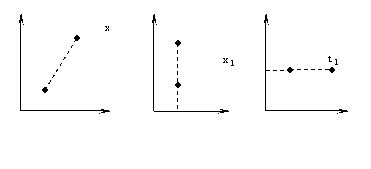
可以从时空图中，直观的看出事件的性质。例如，同地异时和同时异地事件。

2. 相对量

具有实际观测意义的是相对量。例如，间隔和间距都是相对量。

再一次强调：只有在S′系中有被观测的对象，并且被观测的对象的时空本征值是x，t。当S′系相对于S系运动时，S′系中的x和t，变成S系中的x′和t′。

现在的问题是，如果S′系中的间隔和间距发生变化，那么这些本征值的相对量的变化，反映在S系中是什么样？当然S′系仍然是相对于S系运动的。

本征值x和t，在S系和S′系中都是相同的，所谓本征值的相对量，是指间距x₂ –x₁。

我们应用公式（15）和（17）得到
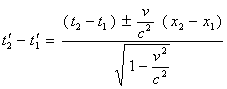               （20）

令

    和   

则有
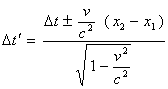                     （21）

上式中，Δt是本征值的相对量，或本征值的变化。而Δt′是Δt在S系中的反映，当然也是相对量，具有可观测性。

应用公式（14）和（16）得到
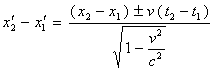                 （22）
　

记
                  
                  

则有
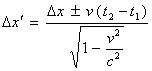                       （23）
　

3. 可观测性条件

虽然相对量具有可观测性，但不是所有的相对量都具有可观测性。

从公式（20）看出，同地性条件为：
　

              （24）

或

        （25）

从公式（22）看出，同时性条件为：

              （26）

或

         （27）

满足上述的条件，才是具有可观测性的事件。