5.3  光行差

1. 经典光行差

经典光行差如图18所示。左图中星光垂直于地面，望远镜能够观测到星光的条件是
                         c﹒Δt = v﹒Δt
即
                                       （49）
　

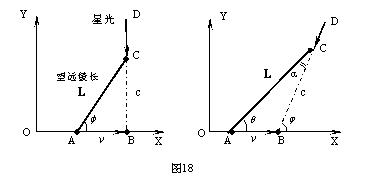
右图中，星光与地面成j 角。在三角形ABC中根据正弦定理，有
                      

                                 （50）
　

根据相对论的观点，当两个系统有相对运动时，上面公式中的Δt将发生膨胀。所以公式（49）是不准确的，必须对它进行相对论修正。

1. 光行差的相对论修正

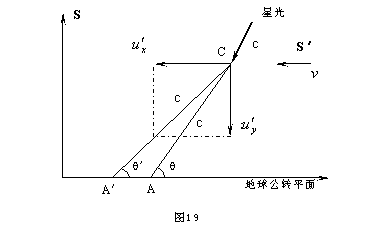
图19是光行差的相对论修正示意图。地球在公转平面上迎着星光运动，速度为 v 。星光与地球公转平面的夹角为j（图18）。望远镜与公转平面的夹角q，相对论修正后的夹角为q′（图19）。

分析：

（1）谁是运动系？光是运动系。

（2）地球是静止坐标系。

（3）相对运动速度v 的方向，与星光的水平速度u_x 相同且平行。

（4）望远镜的长度为CA，光线经过CA的时间极短。相当于光与光影同步，符合洛仑兹变换条件。

（5）CA′是光线真实到达目镜的路径，它一定有两个速度分量，即

    和   。

其中
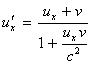                                       （51）

         

上式中，u_x 与 v 平行且方向相同，故用公式（42）。

推导：

仿照经典力学的处理方法，光线是从CA进入到目镜中，这时光线CA的分量为

代入（51）中，得
                   

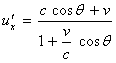
从图中看出，速度的绝对值之比为

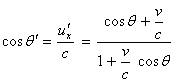
应用近似公式（44），有

展开上式，略去，再代入  得
                             （52）

记光行差为  或    则
                 

上式中，e 为微量，所以  和 ，于是上式变为
                               （53）

式（52）与（53）比较，得
                                       （54）
　

当地球运行到公转轨道的另一端时，地球背离星光运动，相对运动速度为–v，仍然得到公式（53）。