第7章  电子的动量

7.5  质速关系

从电子动量的洛仑兹变换推导出质速公式，整个过程没有什么不符合逻辑的地方。这样，证明了这个理论与实验是一至的。

1. 微观粒子的质速关系

中性粒子和带电粒子统称为微观粒子，简称为粒子。

从微观粒子的引力物质的动量遵从洛仑兹变换的假定，得出中性粒子遵从洛仑兹变换，中子的总质量或惯性质量遵从质速公式。

从电子导出的质速关系是公式（62），即

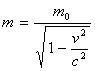
也适合中子。中子的静质量是m₀，惯性质量是m，也是粒子的总质量。不必追问惯性质量m是如何获得的，m只是动量的参数。

这个质速关系是相对于观测者而言的。在某种意义上，观测者相当于绝对静止的背景空间，或是质心。

2. 质量的本征值

这里所说的质量本征值是对一切微观粒子而言的。前面说过，电子质量的的本征值是m₀，它在任何惯性系中都有相同的值。同理，中子质量的本征值也是m₀。所以说微观粒子的质量本征值是m₀。

当电子与观测者相对静止，并且同处于失重状态下，这时引力质量m₀等于0。这种情况下，测定电子的惯性质量，其数值仍然是引力质量m₀。这表明，失重状态下，引力质量并不为0，它仍然以惯性质量数值存在着。可见，质量的本征值是m₀。

结论是：

一切微观粒子，质量的本征值都是引力质量m₀。因为我们生存在引力世界这个层面中。

3. 质速关系的本质

（1）电子被电磁场加速，实质上是电荷被加速。与电荷对应的电磁惯性质量不遵从牛顿第二定律：

而是遵循

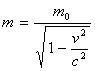
显然，电磁惯性质量与引力惯性质量的惯性性质是不同的，这是可以理解的。因为引力物质与电磁物质毕竟是两种不同属性的物质。

（2）前面，我们不仅接受了

引力质量 = 引力惯性质量

的结论，并认定引力质量m₀是本征值，又特别强调了电子的引力性质在任何相互作用中不变，即引力质量不变。

如果不是这样，将会产生无法克服的矛盾。例如，电子的速度接近光速时，它的引力质量将变为无限大。于是，与电子相对运动的物质和观测者将被电子吸引到自已的周围，事实上这种事情从未发生过。

（3）从质谱仪测出的电子质量是惯性质量，不是引力质量。所以，没有任何理由和证据表明电子的引力质量和引力惯性质量是可变的。

（4）质速关系的本质提示我们，电荷的惯性性质不同于宏观物体的惯性性质。

经典惯性性质是，力与加速度成正比，且永远成正比。与相对运动速度无关。

电磁惯性性质是，惯性大小与相对运动速度相关。

（5）本书没有苛意使用电磁惯性质量一词，而是使用惯性质量，或总质量。这样作的目的之一是便于把质速关系推广到中性粒子。此外，我们对电磁质量的了解不十分清楚，同时它也没有得到物理学的公认。

实质上，电磁相对论恰好是微观粒子的论理，这是始料未及的。

（以上是书上的原文,第7章至到结束）

这一节的重点，是强调 物质 的

惯性性质

不同的物质有不同的惯性性质。

宏观物体的惯性性质为

牛顿力学

电磁物质（电荷）的惯性性质是

相对论力学

即非线性关系。

什么  高速向低速过渡，  向小姨子过渡

只有电子的高速向电子的低速过渡，

不能从电子向宏观物体过渡。

没有道理嘛。

两个不同性质的东西，怎么过，

过了， 就是  不正当关系。

同时

我们看出

用 电磁动量 的 洛仑兹变换

求出

质速关系

是

建立相对论力学的正确方法而且
简捷

恰好  冯天岳  一贯喜欢  投机取巧  这次又让他瞎猫碰上死耗子

现在，回过头来看

托尔曼  假想碰撞实验

不成体统

闹剧

是不是

相对论很简单，一致性很好。

统观全局

很

优美