六、视平均绝对星等

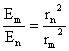
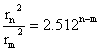
（六）视平均绝对星等

亮度决定于光源的发光功率和观测者距离光源的远近。

视感人类的视觉特性是，当亮度增加一倍时，光感并不增加一倍。经过心理学家的研究得出的规律是
			（50）
式中m 是光感（星等），dm 是光感的变化；E 是亮度，dE 是亮度的变化；c 是比例常数。负号的意义是亮度减小时星等的数值增大。
积分（50）式，得

其中C 是积分常数。对于其它的光源也有同样的公式：

两式相减得

也可以写成

取 m₀ -m =1,2,3,4 .....,可得

这表示，当亮度以几何级数变化时，光感（视星等）则以算术级数变化。当两颗星的星等分别为m 和n ，则有

或

常数K 由观测决定。

视星等早期天文学家把天上最亮的恒星定为1等星，最暗的也就是肉眼刚刚能够看到的星定为6等星。根据观测知道1等星的亮度是6等星的100倍，于是得到

所以
			（51）
和

上式的意义是明显的，当1等星的亮度是2等星的2.512倍时，人的感觉是1等星比2等星亮一倍。这里要注意的是，亮度与明亮的程度（光感）的区别。亮度是眼睛接受到的辐射功率，而明暗的比较是人的神经功能。

绝对星等把一颗星放在离我们10秒差距（pc ）的地方，它所呈现的视星等定义为绝对星等，用字母M 表示。有一颗星，当它的视星等为m 时，与我们的距离是 r_m ，把它移到距离为 r_n 的地方，它的视星等变成 n 。由光学知道，亮度与距离的平方成反比：

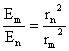
但是，亮度与视星等有关系（52），于是

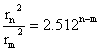
按着绝对星等的定义，有

式中r是任意距离，单位是 pc ；m 是对应于 r 的视星等。通常写成

当 r 的单位是Mpc 时，上式成为

即

本书中的 r 一律用Gpc, 故有公式（41 ）。

视平均绝对星等各个星系的绝对星等是不同的，把所有的星系的绝对星等取算数平均值，就得到平均绝对星等M 。由于这里指的是视星等，所以叫视平均绝对星等M_v 。虽然每一个星系，它的绝对星等并不是平均值，但是平均值对它却有一定的代表性。